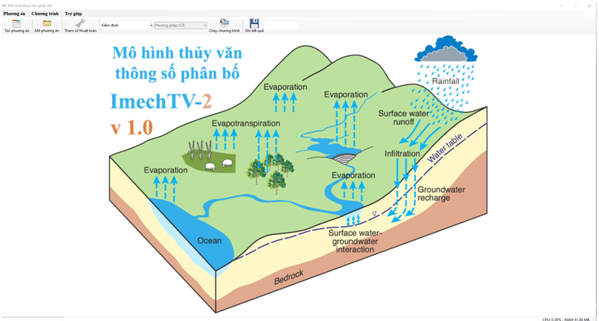
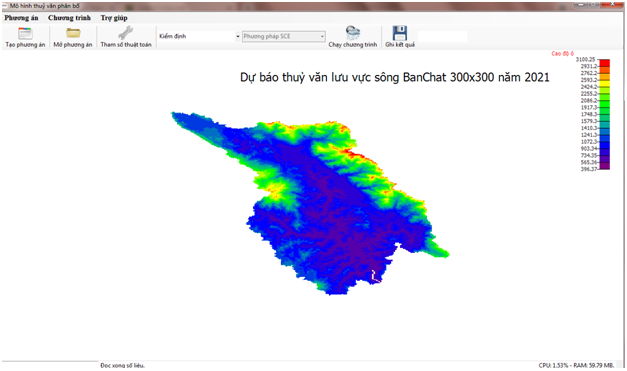
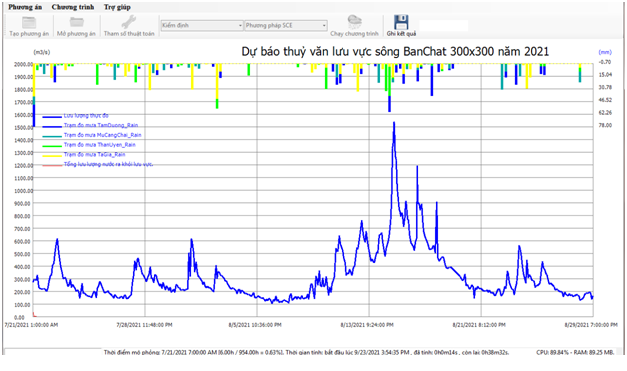
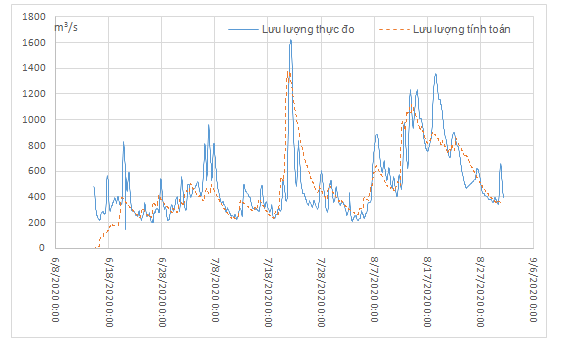
Mô hình thuỷ văn phân bố Imech-TV2
Mô hình thuỷ văn IMECH-TV2: Phát triển mô hình thủy văn tham số phân bố MARINE, cải tiến việc gán mưa theo 03 phương pháp, tính toán song song trên CPU và GPU giúp bài toán có thể chia ô lưới mịn, sử dụng 06 phương pháp ước lượng tham số tối ưu.
- Mưa được gán theo 03 phương pháp:
+ Trực tiếp từng ô lưới.
+ Phân chia theo đa giác Thiessen.
+ Nội suy Kriging.
- Mô hình tự động hiệu chỉnh các tham số bằng 06 phương pháp ước lượng tham số tối ưu giải bài toán ước tính thông số tối ưu cho mô hình thủy văn Marine:
+ Phương pháp ô vuông: Có nhiều phương pháp lựa chọn giá trị tối ưu của thông số nhưng dễ hiểu hơn cả và tính toán vất vả hơn cả là phương pháp ô vuông (phương pháp lưới). Chia miền xác định của từng thông số thành các phần bằng nhau. Với mỗi bộ điểm tại các nút xác định một bộ thông số của mô hình. Thực hiện n lần tính toán theo mô hình để tìm miền có giá trị nhỏ nhất của hàm mục tiêu. Quá trình cứ như thế tiếp diễn cho đến khi bước dò tìm nhỏ hơn một vô cùng bé chọn trước. Phương pháp này chỉ cho phép phát hiện cực trị địa phương đủ rộng hơn mắt lưới, do đó mặc dù đã chấp nhận khối lượng tính toán khổng lồ nhưng vẫn có khả năng rơi vào cực trị địa phương.
+ Phương pháp Rosenbrock: là bước phát triển của phương pháp độ dốc, rất thích hợp với dạng hàm mục tiêu không tính được đạo hàm riêng phần. Chọn sơ bộ mỗi thông số một giá trị hợp lý nào đó, tínhgiá trị của hàm mục tiêu ứng với các giá trị của thông số được chọn lần đầu. Chỉ thay đổi giá trị của một thông số, giữ nguyên tất cả giá trị của các thông số còn lại, tính giá trị mới của hàm mục tiêu. Nếu hàm mục tiêu có giá trị nhỏ hơn tại vị trí cũ, chọn ngay giá trị của thông số vừa tính thử làm giá trị chính thức, còn ngược lại thay đổi giá trị thông số đó theo quy luật tịnh tiến. Lặp lại cho từng thông số và đánh giá hàm mục tiêu sau mỗi lần thực hiện với tất cả các thông số, dừng thực hiện khi bước thay đổi các thông số đều nhỏ hơn 1 giá trị cho trước.
+ Phương pháp Nelder-Mead: sử dụng một mô hình hình học gọi là simplex để di chuyển đi mò điểm tối ưu trong không gian tìm kiếm nên nó được gọi là “Simplex search method”. Các simplex n-chiều này được biến dạng nhờ 3 phép biến đổi: đối xứng gương, phép co, phép dãn dựa vào 4 tham số cần xác định đó là: hệ số phản xạ, hệ số dãn C, hệ số co D và hệ số thu hẹp E.
+ Phương pháp Hooke-Jeeves: là thủ tục dò tìm địa phương: xuất phát từ một điểm x ∈ Rn theo 2n hướng dọc theo n trục tọa độ với độ dài bước h tìm điểm x’ có giá trị hàm mục tiêu f(x’) tốt hơn f(x).
+ Giải thuật di truyền: Giải thuật Di truyền áp dụng quá trình tiến hóa tự nhiên (vận dụng các nguyên lý của tiến hóa như di truyền, đột biến, chọn lọc tự nhiên, và trao đổi chéo) để giải các bài toán tối ưu trong thực tế (từ tập các lời giải có thể ban đầu thông qua nhiều bước tiến hóa hình thành các tập hợp mới với lời giải tốt hơn và cuối cùng sẽ tìm được lời giải gần tối ưu)
+ Phương pháp tiến hóa xáo trộn phức hợp (Shuffled Complex Evolution-SCE): được xây dựng dựa trên: sự kết hợp giữa phương pháp Downhill Simplex của Neader Mead (1956) với các khái niệm của phương pháp tìm kiếm ngẫu nhiên có kiểm soát (Price, 1987); sự xáo trộn cạnh tranh (Holland, 1975); xáo trộn các phức hợp. Phương pháp SCE được khởi tạo bằng cách chọn các tham số p và m với p là số phức hợp, m là số điểm trong mỗi phức hợp. Không gian mẫu s là mẫu lấy ngẫu nhiên trong không gian khả thi của thông số sử dụng một phân phối xác suất thống nhất và tính toán giá trị hàm mục tiêu tại mỗi điểm đó. Sau đó, các điểm trong s đều được sắp xếp theo thứ tự giá trị của hàm mục tiêu tốt dần. Các điểm này sẽ được chia thành p phức hợp, mỗi phức hợp gồm m điểm. Mỗi phức hợp sẽ tiến hóa theo một cách độc lập theo phương pháp Downhill Simplex. Bước tiếp theo, xáo trộn, kết hợp các điểm trong các phức hợp đã phát triển thành một tập mẫu mới dựa trên thông tin của tập mẫu ban đầu. Sự phát triển và xáo trộn này sẽ được lặp đi lặp lại cho tới khi nào các tiêu chí hội tụ được thỏa mãn.
- Mô hình tự động xử lý GIS không dùng phần mềm thứ 3 như ArcView (Fill DEM - thuật toán Planchon và Darboux, Flow Direction, Flow Accumulation).
- Mô hình sử dụng các kỹ thuật tính toán song song tiên tiến giúp giảm thời gian xuống hàng chục lần, thử nghiệm nhiều lần với nhiều thuật toán dò tìm cho nhiều lưu vực khác nhau, nghiên cứu này đã giúp cho quá trình tác nghiệp dự báo được tốt hơn khi có thể tận dụng các ưu nhược điểm của từng phương pháp để áp dụng cho từng lưu vực cụ thể.
- Đặc biệt là hướng xử lý sử dụng phương pháp khối hữu hạn giải phương trình nước nông Saint Venant 2 chiều đầy đủ (mô hình Marine chỉ sử dụng giả thiết đơn giản vận tốc ô lưới là hàm của mực nước) - thay đổi toàn bộ hệ phương trình xuất phát.
- Mô hình thủy văn tính toán được điều tiết dòng chảy, khai thác nguồn nước cho phát điện, giao thông thủy, tưới (nhất là ở vùng khô hạn), cấp nước, quản lý nguồn nước, chất lượng nước.
- Tính toán thủy văn để phòng tránh được các hiện tượng nguy hiểm trên sông như lũ, lụt, hạn hán,... cũng như rất quan trọng đối với phục vụ các hệ thống thủy nông, phục vụ thi công và khai thác công trình thuỷ điện, phục vụ tưới tiêu, phục vụ giao thông đường thuỷ.
- Số liệu đầu vào: diện tích lưu vực, số liệu bốc hơi, số trạm đo mưa, bản đồ phân bố mưa, bản đồ DEM, bản đồ thảm phủ, bản đồ sử dụng đất, …