Our Products and Services
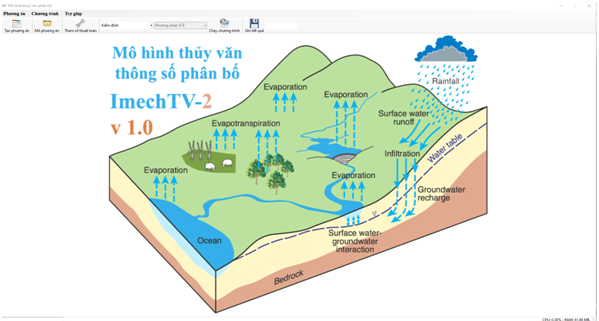
ImechTV2
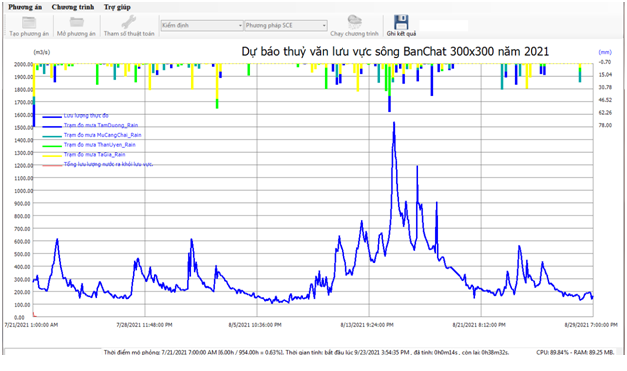
The hydrology model, IMECH-TV2: Developing from distributed- parameters hydrology model,MARINE , improving the attribution of rain according to 03 methods, parallel calculation on CPU and GPU to help the grid can be divided smoothly, using 06 optimal parameter estimating methods.
Rain is assigned according to 03 methods:
+ Directly to each grid.
+ Divided by Thiessen polygon.
+ Kriging Interpolation.
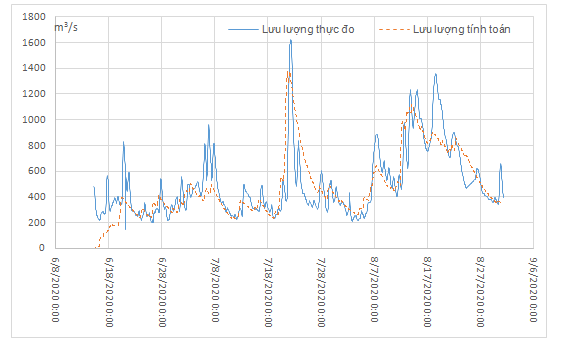
- The model automatically calibrates the parameters by using 06 optimal parameter estimating methods to solve the optimal parameter problem for Marine hydrology model:
+ Square method: There are many methods of choosing the optimal value of parameters but the most easy to understand but hardest to calculate is the square method (grid method). Divide the defined domain of each parameter into equal parts. With each set of points at the buttons determine a set of parameters of the model. Perform n-time calculations to find the domain with the smallest value of the target function. The process continues until the search is smaller than a chosen value. This method only allows for the detection of local extrme that wider than the grid, so despite accepting the huge amount of computation, it is still likely to fall into the local extreme.
+ Rosenbrock method: is the development of the slope method, which is very suitable for the target function form that does not calculate its own derivative. Preliminary selection of each parameter a reasonable value, the value of the target function corresponds to the values of the parameter selected for the first time. Only change the value of one parameter, keep all the value of the remaining parameters, calculate the new value of the target function. If the target function has a smaller value at the old location, immediately select the value of the parameter that has just been calculated as the official value, while changing the value of that parameter according to the law of purification. Repeat each parameter and evaluate the target function after each execution with all parameters, stop performing when the step of changing the parameters is less than a given value.
+ The Nelder-Mead method uses a geometry model called Simplex to find the optimal point in the search space so it's called the "Simplex search method.". These n-dimensions Simplex are deformed by 3 transformations: mirror symmetry, contraction, stretching based on 4 parameters to be determined: reflectivity,elasticity coefficient C, contraction coefficient D and narrowing coefficient E.
+ Hooke-Jeeves method: is a local detection procedure that derives from a point x ∈ Rn in 2n directions along the coordinate axis with step length h to find point x' that has a better target function value f(x') than f(x).
+ Genetic algorithms: apply natural evolution (applying the principles of evolution such as genetics, mutations, natural selection, and cross-exchange) to solve optimal problems in practice (from the set of possible initial solutions through many evolutionary steps that form new sets with better and final solutions. We'll find the best solution).
+ Shuffled Complex Evolution (SCE): builts on a combination of Neader Mead's Downhill Simplex method (1956) with the concept of a randomized controlled search method (Price, 1987); competition turmoil (Holland, 1975); Shuffle the complexes. The SCE method is initiated by selecting the parameters p and m with p as the complex number, m being the score in each complex. Sample space s is a sample taken randomly in the feasibility space of the parameter using a unified probability distribution and calculating the target function value at each of those points. After that, the points in the s are arranged in order of value of the good target function. These points will be divided into p complexes, each of which consists of m points. Each complex will evolve in an independent way using the Downhill Simplex method. The next step, shuffling, combines points in the complexes that have evolved into a new sample set based on the information of the original sample set. This development and disturbance will be repeated until the convergence criteria are satisfied.
- The model does not use third software such as ArcView (Fill DEM - Planchon and Darboux algorithm, Flow Direction, Flow Accumulation).
- The model uses advanced parallel computing techniques that reduce calculating time, repeatedly tested with many detection algorithms for many different basins, this study has made the forecasting process better when it can take advantage of the advantages and disadvantages of each method to apply to each specific basin.
- Especially the using the finite block method of solving the full 2-D Saint Venant shallow water equation (Marine model only uses the simple assumption that grid velocity is the function of the water level) - changing the entire system of starting equations.
- The hydrology calculation to regulate the flow, exploit water sources for electricity generation, water traffic, irrigation (especially in dry areas), water supply, water source management, water quality.
- The hydrology calculation to prevent dangerous phenomena in rivers such as flash floods, floods, droughts,... as well as very important for serving irrigation systems, serving the construction and exploitation of hydropower works, serving irrigation, serving waterway traffic.
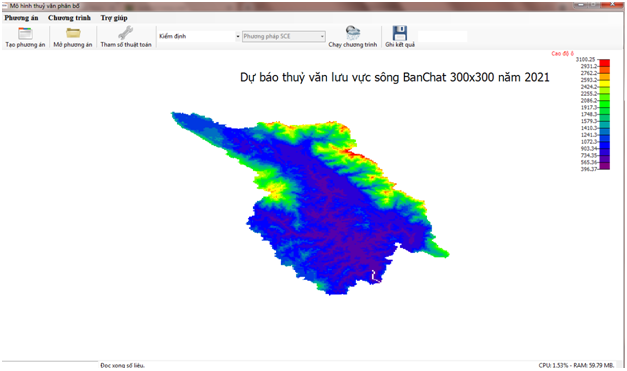
- Input data: basin area, evaporation figures, rainfall stations, rain distribution maps, DEM maps, carpet cover maps, land use maps, ...